本篇笔记是对3b1b神经网络系列视频的简短摘要备忘,主要以名词解释来串联视频内容。
系列网站:3Blue1Brown | Neural Networks b站有官方翻译双语字幕视频。
3b1b推荐拓展学习书目:
视频:
博客:colah’s blog(关于神经网络和拓扑学的博文写得很好)
But what is a Neural Network? #
- Hidden layers: 隐藏层是神经网络中介于输入层和输出层之间的层级。这些层级通常包含了大量的神经元(或节点),并用于处理和转换输入数据以生成网络的输出。
- Why use layers?
- because Layers Break Problems Into Bite-Sized Pieces
- How Information Passes Between Layers?
- Why use layers?
为什么要这么简写公式,并且这种矩阵表示很重要?
These days, due to the demand for more machine learning and more powerful networks, there have been huge improvements in specialized hardware, making for much faster matrix multiplication, for example, Google’s “Tensor processing unit”, or TPU.
Half the time when you hear a company describe something like a “new neural architecture” meant for more powerful AI, what they really mean, when you look under the hood, is that they’re multiplying matrices more quickly.
In fairness, this hardware often does more than just multiply matrices, but that’s the main difference. And if you understand the above section, you understand why.
简单来说,就是所谓“优化神经架构”,半数时候是指优化矩阵相乘速度。
- bias: 偏差、偏置。在上面的公式中,“$-10$”就是bias。也就是说,并不是公式结果大于0就活跃,而是在大于10时才“有意义地活跃”。因此,偏置的作用是在模型的预测中引入一个固定的偏移量,以便更好地拟合训练数据。
- Neurons: a thing that holds a number–>a function (that uses all its weights and biases to take in input pixels and spit out output numbers.)
下一节课:How does this network learn the appropriate weights and biases from data?
Gradient descent, how neural networks learn #
Gradient descent, how neural networks learn 相关课程(多变量微积分):Multivariable Calculus | Khan Academy
- The “learning” of [[About Machine Learning|machine learning]]: The process of learning is essentially just finding lower and lower points on a specific function.
- Weights and biases:根据前面总结出的公式,可以说神经网络的行为是由其所有权重和偏置决定的。权重表示一层中每个神经元与下一层中每个神经元之间的连接强度,而每个偏置都表示其神经元倾向于活跃还是不活跃。
- So, how the network learns?
- 首先,将所有权重和偏置初始化为随机数。
- Then how do you programmatically identify that the computer is doing a lousy job and then help it improve?
- Define a cost function.
- So, how the network learns?
- the Cost Function: 成本函数是用以衡量假设函数准确性的工具。该函数也被称为“[[损失函数]]”、“平方误差函数”或“均方误差”。公式形如:$\lambda(x)=C(t-x)^2$ ,其中t为目标函数,$C$为与决策无关的常数。其他相关内容可参见最小二乘法。
- the “cost” of a single training example: 将每个输出值与您希望它们具有的值之间的差取平方后相加
- The Cost Over Many Examples: The cost function is a layer of complexity on top of neural networks which is a complicated function itself.
- How to find an input that minimizes the value of this cost function?:
- 先考虑只有一个输入的情况:
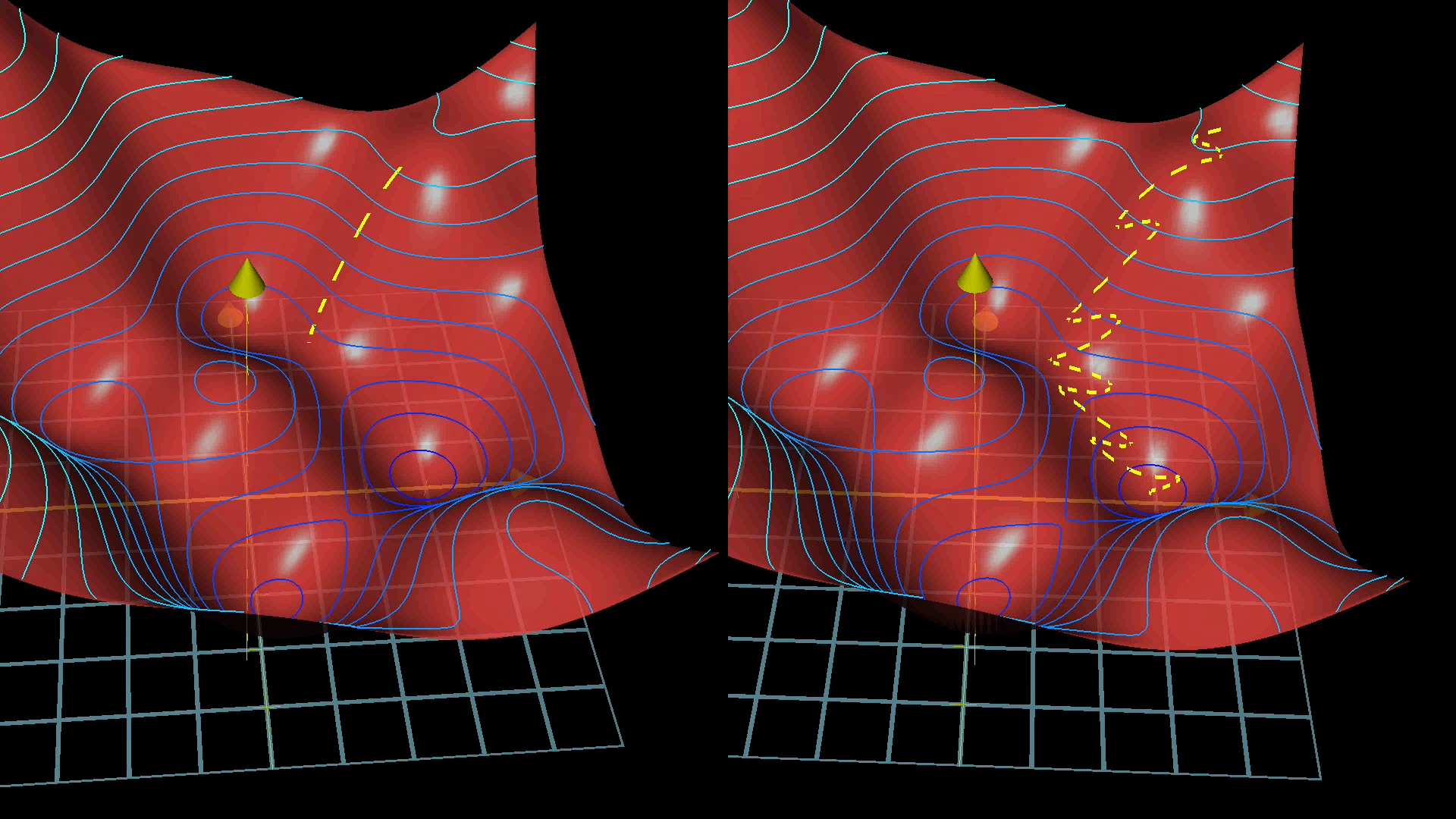
- 对于过于复杂的函数,并不能用微积分中计算斜率的方式来获得最小值。更方便的方式是从随机输入开始,找出应该采取的方向来降低输出,最终找到函数的某些局部最小值。
- 注意:可以调整步长与坡度,使之成正比,来防止overshooting。
- 再稍微提高复杂度,考虑有两个输入一个输出的情况:
- You might think of the input space as the xy-plane, with the cost function graphed as a surface above it.
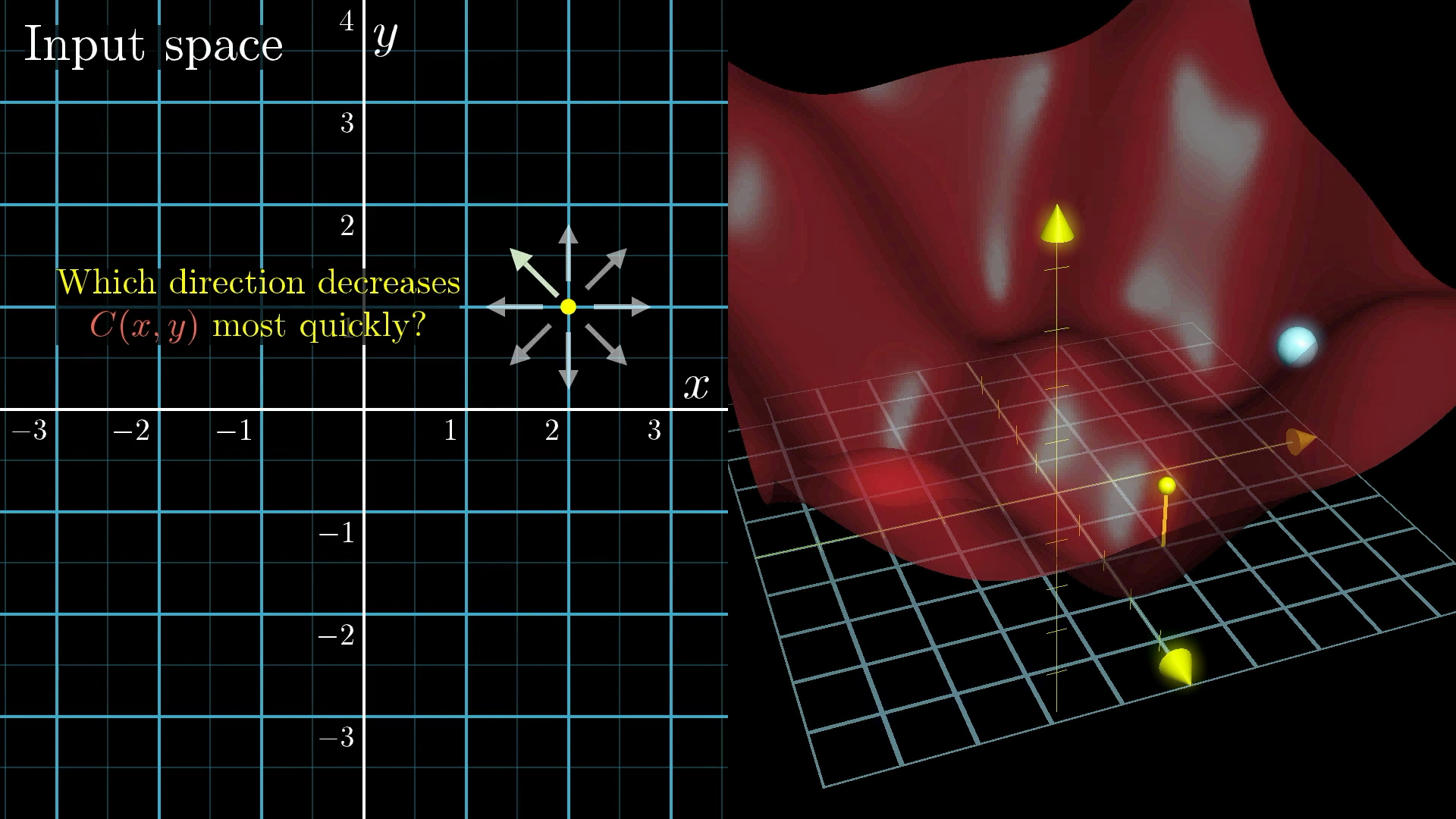
- You might think of the input space as the xy-plane, with the cost function graphed as a surface above it.
- 先考虑只有一个输入的情况:
- gradient: 梯度。在高维空间中,应该使用向量来表示direction of steepest ascent/descent。这个向量被称为梯度。
- Gradient descent: 梯度下降法。要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。
- Another Way to Think About The Gradient:
- 可以将整个网络的所有权重和偏置想成一个包含n个条目的大列向量$\vec w$。那么成本函数的负梯度也将是一个有 n个条目的向量$- \nabla C(\vec w)$。
- The negative gradient: 负梯度向量$- \nabla C(\vec w)$,是负梯度上述的极其巨大的输入空间中的一个向量方向,指向让成本函数最快速的下降的方向。鉴于成本函数其实是包含着参数与权重的函数,所以其值的下降意味着模型有更好的表现。
- 有效计算梯度向量值的算法称为反向传播(backpropagation),之后的课程会讨论。
- 梯度的符号告诉我们向量的相应分量是否应该向上或向下微移,而梯度中各分量的相对大小告诉我们哪些变化更重要。因此可以说,大规模成本函数的梯度编码了每个权重和偏置的相对重要性。
- 由此可以认为:If the cost function is a layer of complexity on top of the original neural network function, its gradient is one more layer of complexity still, telling us what nudge to all these weights and biases causes the fastest change to the value of the cost function.
- 正因为所谓的“学习”指的是改变权重和偏置以最小化成本函数,所以成本函数需要良好且平滑,以便我们可以通过采取许多小步长下坡来有效地找到局部最小值。
- 顺便说一句,这就是为什么这些人工神经元具有连续范围的激活,而不是像生物神经元那样简单地处于活动或不活动状态。
“最近”(视频发布于2017年10月)的几篇关于图像识别领域神经网络工作原理的论文:
- Understanding deep learning requires rethinking generalization
- A Closer Look at Memorization in Deep Networks
- The Loss Surfaces of Multilayer Networks
Analyzing our neural network #
神经网络在“学习”时,实际上并不会像我们可能假设的那样,用“Break number into small pieces”的方法(例如识别出一个⭕和直线的组合后判断是数字9)来判断数字。
如果将神经网络中层与层之间传递的权重可视化为如图所示的这种像素模式,我们不难发现它们看起来几乎是随机的,而不像预想中那样是数字拆解出来的小片段。可能其中有一些松散的模式,但绝非我们所期望的那样。

Much of this is because it’s such a tightly constrained training setup. From the network’s point of view, the entire universe consists of nothing but clearly defined unmoving digits centered on a tiny grid, and its cost function never gave it an incentive to be anything but utterly confident in its decisions.
当然,目前演示使用的是一个比较老、比较基础的神经网络,在很多功能方面都有局限。还有很多现代变体可供之后继续学习、探索。
What is backpropagation really doing? #
What is backpropagation really doing? 如前所述,梯度的每个分量的大小告诉我们成本函数对每个相应的权重和偏置的敏感程度。因此这节课不使用数学符号,而通过展示训练示例对权重和偏置的影响,来让观众更直观地了解反向传播算法。
Hopefully, these effects will feel intuitive so that by the time we return to the notation, it acts to articulate something you already know, rather than acting as a code to be decrypted.
- Backpropagation: 反向传播算法,是一种计算负梯度的算法(数学上来说,其实是多元函数求偏导)。
在神经网络训练中,由于最初的权重和偏置都是随机的,所以最初的输出和我们期望的值毫无关系。要使输出趋向于期望的数值(以数字2为例),就需要调整激活2的权重使其变高,而使其他数字的值趋向0.
这些微调的大小应与每个输出值距目标的距离成正比。偏离较远的神经元需要大的推动,但非常接近正确的神经元只需要很小的推动(nudges)。
如前所述,公式为:$\sigma(w_1 a_1+w_2 a_2+...+w_n a_n-b)$,所以有三个途径来调整激活:
- Increase the bias
- 改变偏差是改变激活的最简单方法。与更改前一层的权重或激活不同,更改偏差对加权和的影响是恒定且可预测的;
- 如果要增加某数字输出神经元的激活,应该增加与之相关的偏差,并减少与所有其他神经元相关的偏差。
- Increase the weights
- 与上一层的激活值有关,上一层激活值越大的神经元在更改权重时造成的影响更大;
- 这令人想起神经科学里的Hebbian theory,因为正是目前激活值高的神经元与我们希望激活值升高的神经元之间权重增加幅度最大。
- Change the activations from the previous layer
- 正如按激活正比例(in proportion to)改变权重一样,通过按相关权重的正比例增加激活,可以获得更大的收益;
- 激活不能直接被改变,要通过更改上一层权重和偏置来改变,但是记下来要如何改变他们很有用!
- 不仅要考虑对期待激活数字,还要考虑期待不被激活的数字。将所有期待的改变相加,就是我们最后获得的对这一层神经元期待的改变。重复这个过程,直到第一层。
而对于要训练的整个模型来说,需要把每个样本需要如何修改weight & bias,最后相加取平均值。最后这样获得的一系列微调weight & bias均值,大约就可以看作是前面提到的负梯度(或者其标量的倍数)。
- Stochastic gradient descent(often abbreviated SGD): 随机梯度下降是梯度下降的变体之一,通常用于大规模数据集和复杂的模型训练中。与传统梯度下降不同,SGD每次迭代中仅使用训练数据的一个子集(随机选择的样本),而不是整个数据集(不然训练时间太长了)。
- Mini-batches: SGD每次迭代中的那个随机选择的子集就是mini-batches。这两种训练方法大致的区别如图所示(不一定更精准,但肯定更快!):
Backpropagation calculus #
Backpropagation calculus 这节课是上节课的微积分版。
Start with a network where each layer has just one neuron #
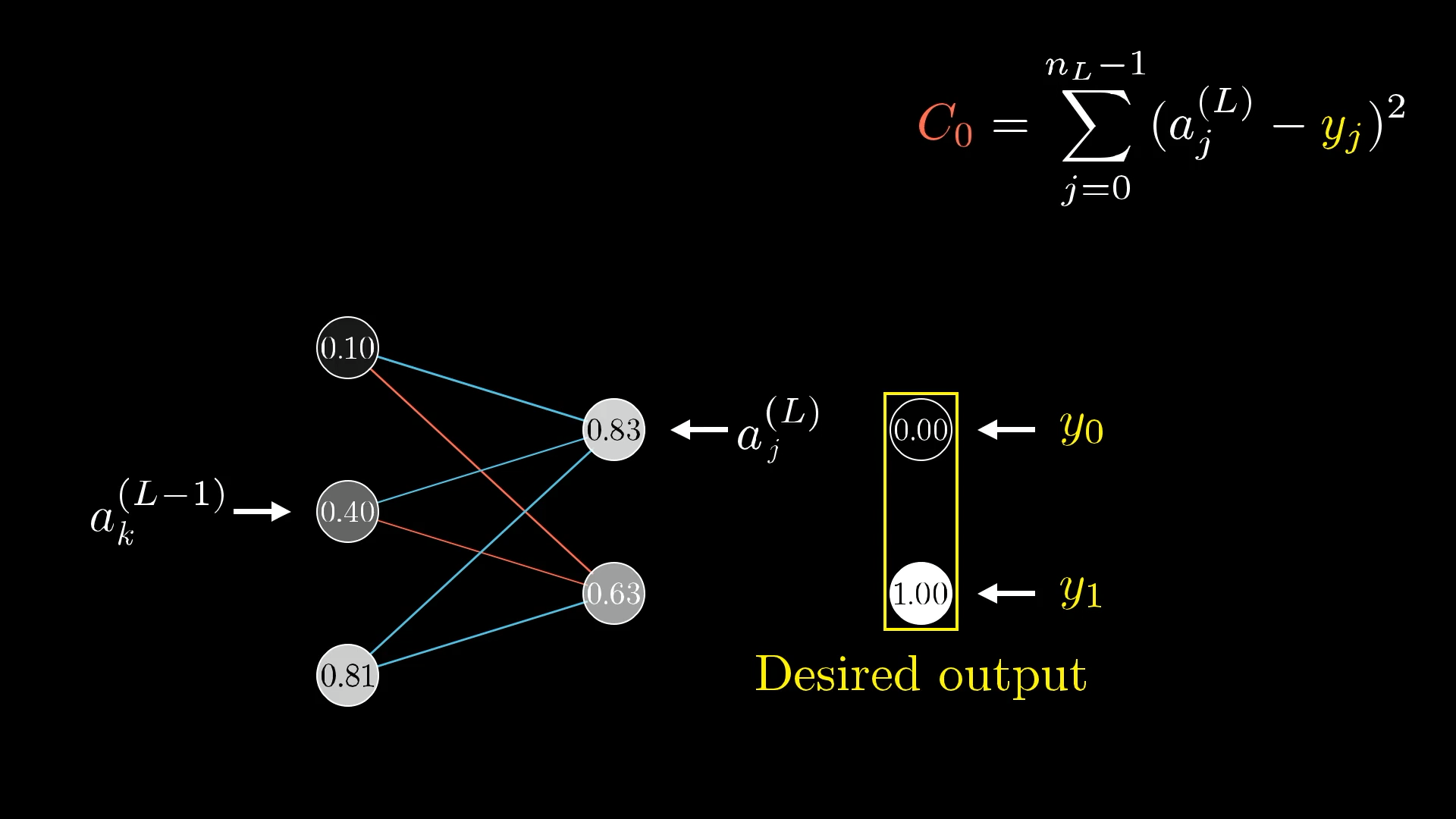
首先设想每层网络只有一个神经元的情况: 可以将某两层神经元的激活数值标记为$a^{(L-1)}$、$a^{(L)}$,其中$L$是神经网络的最后一层总层数(注意不是指数!)。 设所需要的输出是$y$,单次训练的成本是$C_0$,那么根据前面已经知道的Cost Function,这一层的训练成本为$C_0 = (a^{(L)}-y)^2$. 又有$a^{(L)}=\sigma (w^{(L)}a^{(L-1)}+b^{(L)})$. 为表达方便,令$z^{(L)}=w^{(L)}a^{(L-1)}+b^{(L)}$,即$a^{(L)}=\sigma (z^{(L)})$.
接下来,通过求导来了解成本对权重的微小变化有多敏感,即求$\frac {\partial C_0}{\partial w^{(L)}}$.
[! What is ∂] $\partial$指偏微分,对于一个多元函数$f(x,y)$,$\frac{\partial f}{\partial x}$相当于固定$y$变量,对$x$进行求导。 $\mathrm{d}$指全微分,对于一个多元函数$f(x,y)$,$\mathrm{d}f=\frac{\partial f}{\partial x}\mathrm{d}x+\frac{\partial f}{\partial y}\mathrm{d}y$.
由于成本对权重变化的反馈可以分解为一系列变化,因此根据前面的等式,可以把刚刚的求导分解为:
$$\frac {\partial C_0}{\partial w^{(L)}}=\frac {\partial z^{(L)}}{\partial w^{(L)}}\frac {\partial a^{(L)}}{\partial z^{(L)}}\frac {\partial C_0}{\partial a^{(L)}}$$分别对分解出来的三项求导,可得:
$$\frac {\partial C_0}{\partial w^{(L)}}=a^{(L-1)}{\sigma}'(z^{(L)})2(a^{(L)}-y)$$这个公式告诉我们最后一层中的某个特定权重的微调将如何影响该特定训练示例的成本。
接下来计算总的成本,也就是每层成本相加取均值:
$$C=\frac 1 n \sum_{k=0}^{n-1}C_k$$所以导数就变成了:
$$\frac {\partial C}{\partial w^{(L)}}=\frac 1 n \sum_{k=0}^{n-1}\frac {\partial C_k}{\partial w^{(L)}}$$这个导数也就是成本函数$C$的其中一项。 要求出完整的梯度:
$$\nabla C=\begin{bmatrix} \frac {\partial C}{\partial w^{(1)}} \\ \frac {\partial C}{\partial b^{(1)}} \\ \vdots \\ \frac {\partial C}{\partial w^{(L)}}\\\frac {\partial C}{\partial b^{(L)}}\end{bmatrix}$$还需要求bias,这个问题不大,只需要把刚刚的求导$\frac {\partial C_0}{\partial w^{(L)}}$替换为$\frac {\partial C_0}{\partial b^{(L)}}$即可。 而对于前一层的权重和偏置,相似的,只需求$\frac {\partial C_0}{\partial a^{(L-1)}}$. 更进一步的,可以求出$\frac {\partial C_0}{\partial w^{(L-1)}}$.根据这样的思想,可以计算整个梯度向量。
More Complicated Networks #
基本没有什么太大区别,只是增加了更多的下标和求和。如图:
作为总结,最终可以计算出负梯度向量:

当然,鉴于通常实际处理会用各种库,因此这里最重要且最通用的理解是如何通过分解依赖链来推断一个变量对另一个变量的敏感性。
Stepping back, if you take away just one idea from this series, I want you to reflect on how even relatively simple pieces of math, like matrix multiplication and derivatives, can enable you to build genuinely incredible technology when put into the right context.
Think about how matrix multiplication elegantly captures the propagation of information from one layer of neurons to the next. Think about how we can take the somewhat fuzzy idea of intelligence, or at least the narrow sliver of intelligence required to classify images correctly, and turn it into a piece of calculus by finding the minimum of a carefully defined cost function. Think about how derivatives and gradients give us a concrete way to find such a minimum (well, a local minimum anyway). Or think about the chain rule, which in most calculus classes comes across as “just one of those tools” that you need for more homework problems, and how in this context it let us cleanly decompose an insanely complicated network of influences to understand how sensitive that cost function is to each and every weight and bias.
关于反向传播微积分的其他资源:
- http://neuralnetworksanddeeplearning.com/chap2.html
- https://github.com/mnielsen/neural-networks-and-deep-learning
- http://colah.github.io/posts/2015-08-Backprop/
But what is a GPT? #
Attention in transformers #
How might LLMs store facts #
待完成。


